Research
Active research topics
Quantum Phase Characterization by Tensorial-Kernel Support Vector Machines
researchers : Nicolas Sadoune, Giuliano Giudici, Ke Liu, Lode Pollet
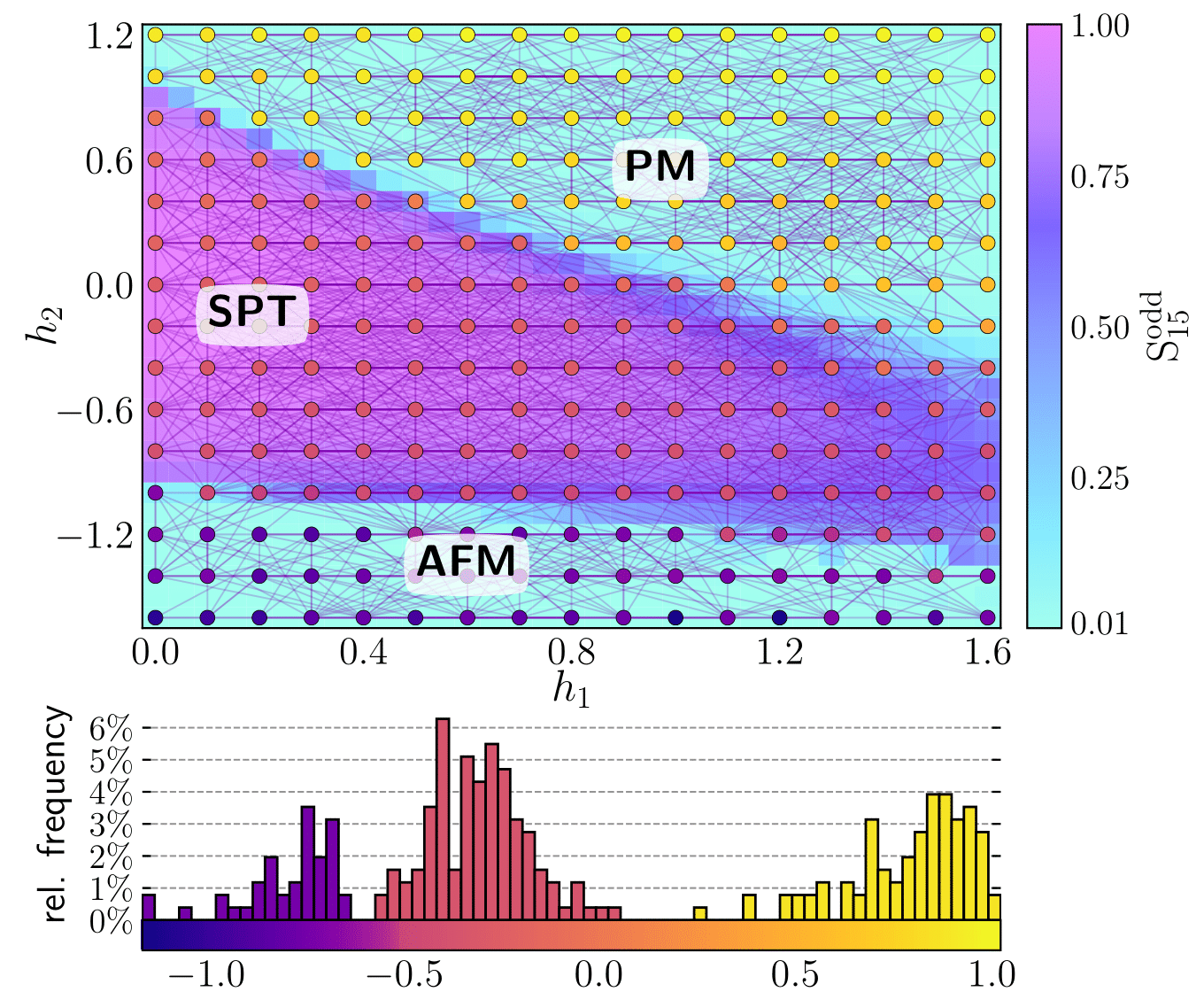 We employ an unsupervised machine-learning technique based on data of local measurements to understand short-range entangled many-qubit systems.
We employ an unsupervised machine-learning technique based on data of local measurements to understand short-range entangled many-qubit systems.
Our method successfully constructs the phase diagram of a cluster-model and detects the respective order parameters of its phases, including string order parameters.
For the toric code subject to external magnetic fields, the machine identifies the explicit forms of its two stabilizers.
Prior information of the underlying Hamiltonian or the quantum states is not needed.
Instead, the machine outputs their characteristic observables.
This work shows machine learning can mature into a trustworthy tool for exploring exotic phases in many-body system
- Phys. Rev. Res. 5, 013082 (2023)
Spin liquids and frustration in Centred Pyrochlore Lattice
researchers : Rajah Nutakki, Ludovic D. C. Jaubert, Lode Pollet
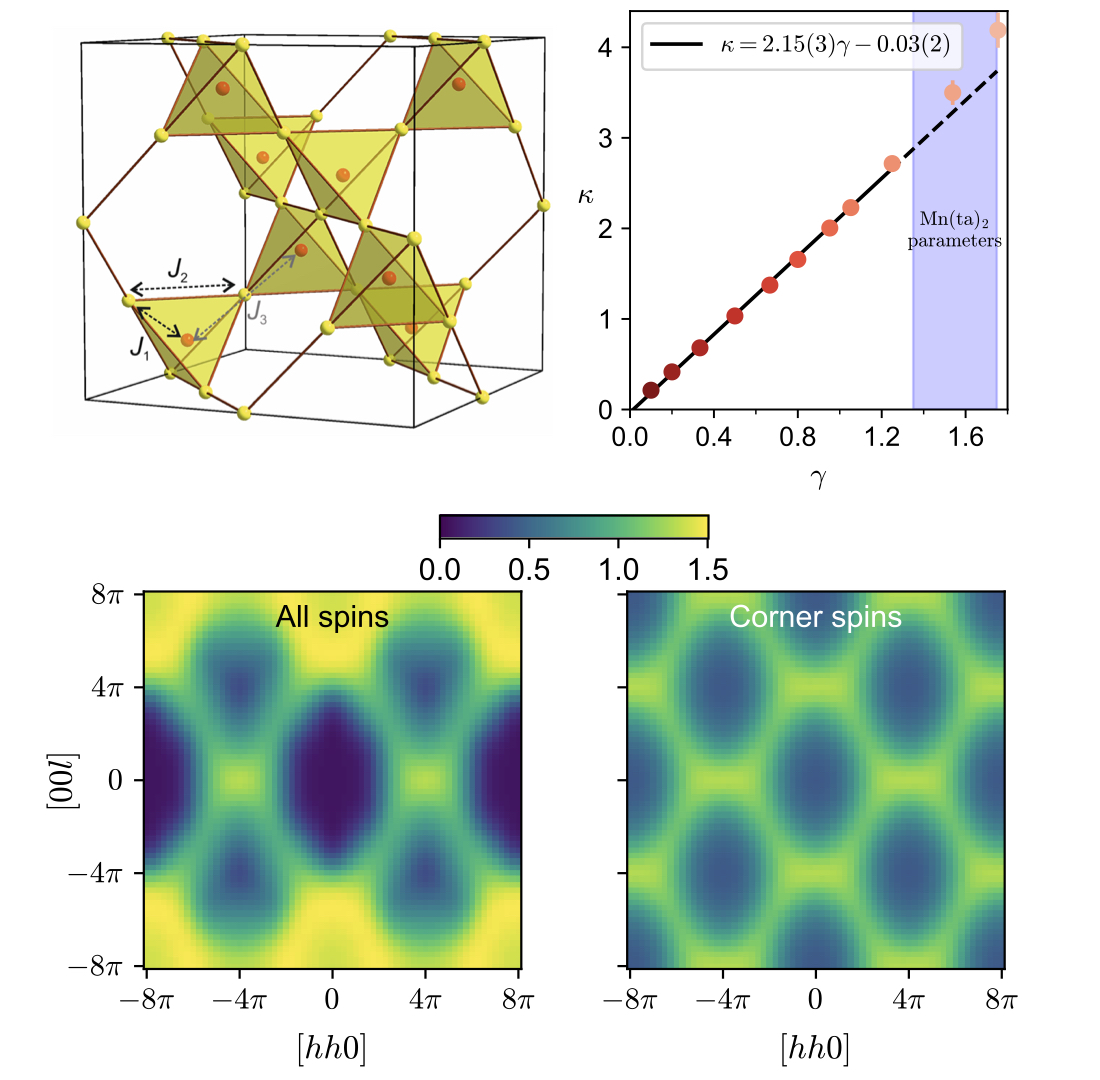 The centred pyrochlore lattice is a novel highly geometrically frustrated model characterized by a rich phase diagram at low temperature. This was identified as the molecular design in metal-azolate framework [Mn(II)(ta)2], with the frustrated regime depending on the interplay between nearest neighbour and next-to nearest neighbour interactions (respectively with interaction strength J1 and J2). Through a combination of analytics, numerics and experiments we found that, at a particular interaction regime, the reciprocal space structure factor S(q) is characterized by finite width bowties, also referred to as pinch points, which are found to arise from the correlations between spins residing at the vertices of the tetrahedra. The width of these bowties was found to scale linearly with the ratio γ ≡ J1 /J2 up to γ=1.25.
The centred pyrochlore lattice is a novel highly geometrically frustrated model characterized by a rich phase diagram at low temperature. This was identified as the molecular design in metal-azolate framework [Mn(II)(ta)2], with the frustrated regime depending on the interplay between nearest neighbour and next-to nearest neighbour interactions (respectively with interaction strength J1 and J2). Through a combination of analytics, numerics and experiments we found that, at a particular interaction regime, the reciprocal space structure factor S(q) is characterized by finite width bowties, also referred to as pinch points, which are found to arise from the correlations between spins residing at the vertices of the tetrahedra. The width of these bowties was found to scale linearly with the ratio γ ≡ J1 /J2 up to γ=1.25.
References:
- SciPost Phys. 15, 040 (2023)
- Phys. Rev. Research 5, L022018 (2023)
Tangle of Spin Double Helices in the Honeycomb Kitaev-Γ Model
researchers : Jheng-Wei Li, Nihal Rao, Jan von Delft, Ke Liu, Lode Pollet
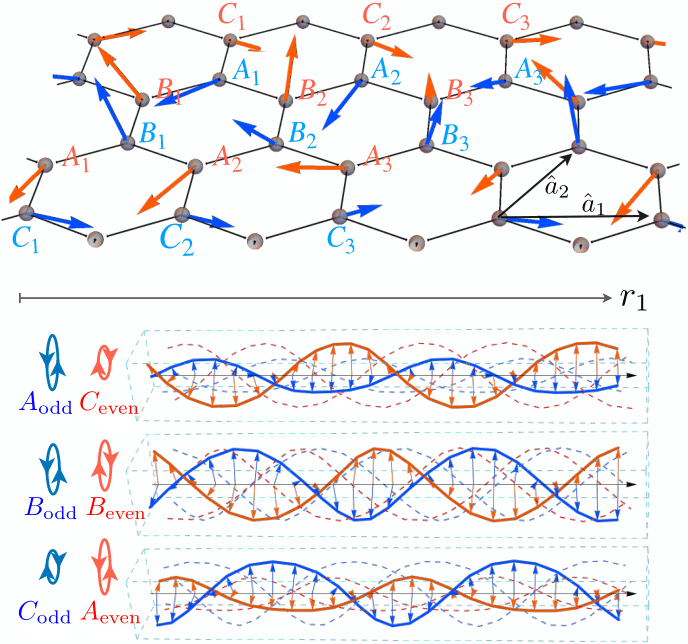
The honeycomb Kitaev-Γ Hamiltonian is a paradigmatic model for the physics of two-dimensional Kitaev magnets. The Kitaev exchange leads to an exactly solvable spin liquid and can be realized in d-electron transition-metal compounds with edge-shared geometry. However, symmetries of real materials permit a generic existence of a Heisenberg and an off-diagonal Γ term which may dramatically modify the desired spin-liquid ground state. Using infinite projected entangled pair states (iPEPS) to investigate the honeycomb Kitaev-Γ model in material relevant regimes, we discovered that the classical ground state imprints a tangle of emergent spin double helices. This unprecedented many-body order is characterized by anisotropic periodicities and a sgn(Γ)-determined chirality pattern. The emergence of this helicity may give rise to peculiar dynamical and transport behaviors, such as spectrum broadening and splitting, long-living currents and anomalous diffusions.
References:
- arXiv:2206.08946
Reliability of Fracton Models for Quantum Error Correction
current researchers : Giovanni Canossa, Hao Song, Ke Liu, Miguel A. Martin-Delgado, Lode Pollet
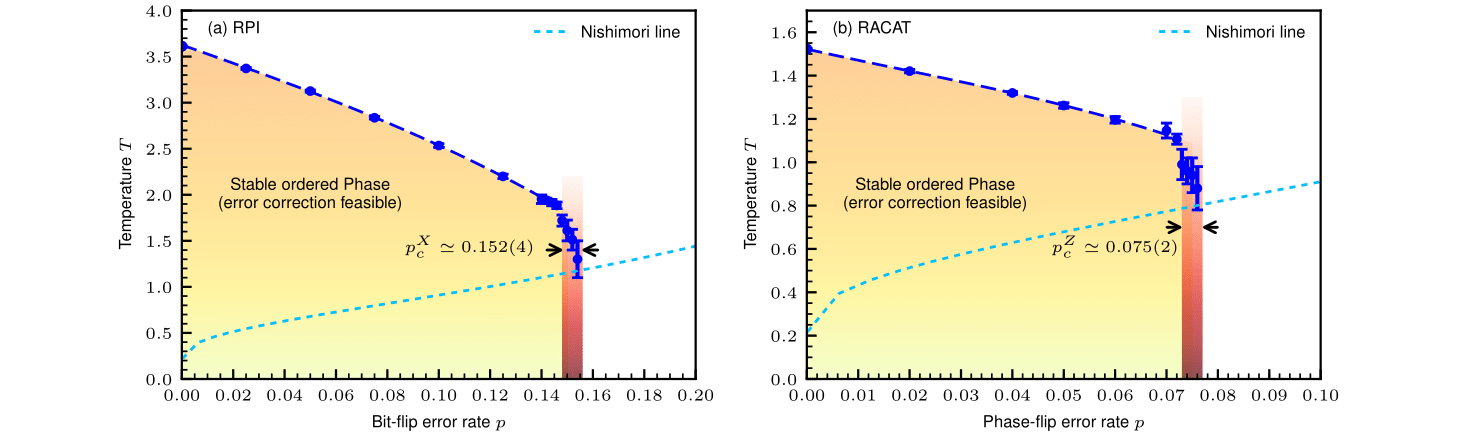
Surface codes are heavily studied in the field of quantum error correction (QEC) due to the high resilience to errors introduced by their characteristic topological protection, which is reflected in their optimal error threshold. So far, toric code and color code are known to offer high error thresholds in 2D. Due to their peculiar interplay between subsystem symmetries and topological order, fracton models represent optimal candidates for efficient QEC in 3D. An example is the X-cube model, which was shown to have a resilience against X- and Z- errors up to an error probability of 15.2% and 7.5% respectively. These results represent a first step towards the investigations of the resilience to errors of different fracton models and bring attention to their theoretical applicability to quantum computation in 3D.
References:
- Phys. Rev. Lett. 129, 230502 (2022)
Investigation of Fracton models using NQS
researchers : Marc Machaczek, Ke Liu, Miguel A. Martin-Delgado, Lode Pollet
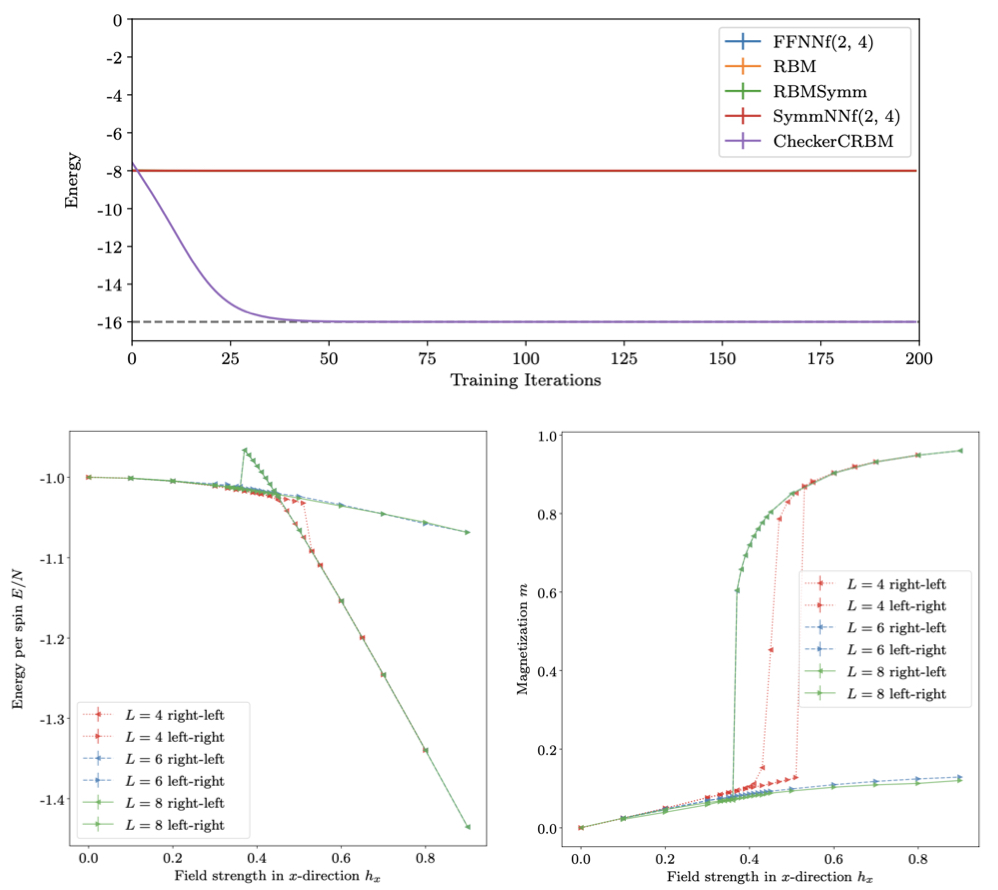
Fracton models recently began to attract a lot of interest due to their rich theoretical description of beyond conventional topological order and their potential use as robust quantum memory. However, the stability of fracton phases with respect to local perturbations is not yet fully explored, partly due to the difficulty of simulating such three-dimensional, highly entangled systems numerically. Using different variations of restricted Boltzmann machines, we were able to succesfully show how neural network quantum states enable the exploration of the phase diagram for the Checkerboard model.
References:
- TBA

