Numerical Methods for Many-Body Systems
Peter Kroiß, Dario Hügel, Sebastian Schulteß and Lode Pollet
Diagrammatic Monte Carlo
Fermi Polaron
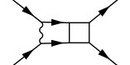
The concept of separating nontrivial problems into a homogeneous background and an impurity is widely used throughout physics. A special case is given by Fermi polarons acting upon a noninteracting Fermi sea. Its physics experiences rich features like the competition between formation of molecules out of impurity and bath particles and standard polaronic behavior.
Diagrammatic Monte Carlo, a numerical technique designed to sample Feynman diagrams, is applied to measure state and quasiparticle properties of the Fermi polaron problem. Instead of directly evaluating all Feynman diagrams, an algorithm is devised that allows to change the expansion order, topology and internal degrees of freedom of a diagram. The method has a sign problem, which however is not volume dependent and can be alleviated with the help of analytical tools. In many cases a precise result can be found by extrapolation and/or resummation of the lowest expansion order results.
Dynamical Cluster Approximation/Dynamical Mean Field Theory
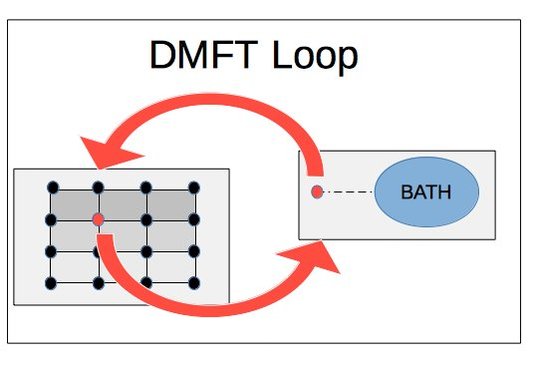Bosonic dynamical-mean field theory (B-DMFT) is a well-established numerical technique for the treatment of bosonic many-body systems in condensed matter, as e.g. the Bose-Hubbard model. However, due to arising numerical instabilities, the application to dynamical out-of-equilibrium problems remains an open challenge. Furthermore, in order to study inhomogeneous or topologically non-trivial systems, an application of the dynamical cluster approximation (DCA) to B-DMFT would be necessary. The purpose of our work is to further develop B-DMFT or B-DMFT-like self-consistencies in order to tackle these problems.