2016-2018
Researchers : Ke Liu, Dario Hügel, Tobias Pfeffer, Sebastian Schulteß, Jonas Greitemann, Janik Schönmeier-Kromer, and Lode Pollet
Physics of Cold Atomic Systems
We are interested in the phenomenology of cold atomic systems in a wide variety of settings. First, we explore the possibilities a microscope offers to the experimental study of cold fermionic samples aiming at identifying novel types of magnetism and superfluidity in Hubbard-like models. Second, we study the behavior of quantum systems in the presence of inhomogeneous conditions, either in space or in time, when they are close to a phase transition. Third, we are interested in the hydrodynamic description of multi-component superfluids and superfluid drag. The main tools are the renormalisation group theory of critical phenomena, numerical simulations (primarily quantum Monte Carlo and exact diagonalization), and the hydrodynamic theory of superfluidity.
Lattice Gauge Theory and Exotic Order
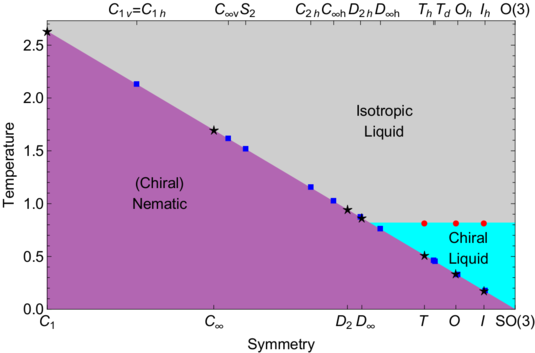 Spontaneously breaking a large symmetry to its subgroups can lead to phases characterized by orders with an internal symmetry. Very often these phases possess non-trivial thermodynamical and topological properties. They are ubiquitous in both classical and quantum systems such as nematic phases in assembly of molecules, fluids of correlated electrons, and systems of spinor atoms. However, they remain largely unexplored, especially for those involving non-Abelian symmetries. We are interested in condensed matter systems and theoretical models that support such phases, in particular their realization in quantum regimes. The methods we use are based on lattice gauge theories, which appear to be convenient and mighty tools when traditional approaches become cumbersome.
Spontaneously breaking a large symmetry to its subgroups can lead to phases characterized by orders with an internal symmetry. Very often these phases possess non-trivial thermodynamical and topological properties. They are ubiquitous in both classical and quantum systems such as nematic phases in assembly of molecules, fluids of correlated electrons, and systems of spinor atoms. However, they remain largely unexplored, especially for those involving non-Abelian symmetries. We are interested in condensed matter systems and theoretical models that support such phases, in particular their realization in quantum regimes. The methods we use are based on lattice gauge theories, which appear to be convenient and mighty tools when traditional approaches become cumbersome.
Diagrammatic Monte Carlo Simulations
The Homogeneous Electron Gas
Many-body calculations for correlated-electron systems pose a long-standing challenge in condensed matter physics. The main difficulty in such calculations stems from the long-range nature of the Coulomb interaction. This, for instance, manifests in a perturbative treatment of the homogeneous electron gas (jellium model), where certain classes of diagrams diverge. From a physical point of view one wants to understand collective phenomena such as the effective screening of the electron-electron interaction. A textbook example of a simple approximation, which tries to capture this physics and partly resolves the divergencies, is the so-called random phase approximation. It turns out to quite accurately reproduce the ground state energy of the electron gas at high densities. However, an accurate solution for a wider range of densities is of crucial interest, as jellium, while itself being a basic model for electrons in a solid, is also the starting point for more elaborate electronic structure calculations within density functional theory.
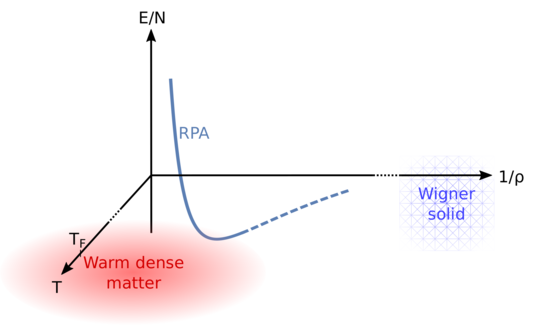 Expanding upon this is the idea of a series of skeleton diagrams, where all divergent contributions are excluded from the series, but are implicitly incorporated via a self-consistent scheme. This self-consistency can be combined with the technique of Diagrammatic Monte Carlo to evaluate higher-order diagrams. We investigate the applicability for various densities and temperatures, from the ground state up to the region of warm dense matter, depending on the convergence (or asymptotic) properties of the underlying series at the given regime.
Expanding upon this is the idea of a series of skeleton diagrams, where all divergent contributions are excluded from the series, but are implicitly incorporated via a self-consistent scheme. This self-consistency can be combined with the technique of Diagrammatic Monte Carlo to evaluate higher-order diagrams. We investigate the applicability for various densities and temperatures, from the ground state up to the region of warm dense matter, depending on the convergence (or asymptotic) properties of the underlying series at the given regime.
Spectral functions of the Froehlich polaron
The interaction of electrons with the crystal lattice gives rise to a multitude of interesting phenomena. The Coulomb attraction between a single impurity and vibrations of the lattice can be described within the Froehlich model, resulting in an expansion in terms of Feynman diagrams where the electron is dressed by phononic excitations, giving rise to a quasiparticle, the polaron, composed of the electron and its surrounding phonon cloud.
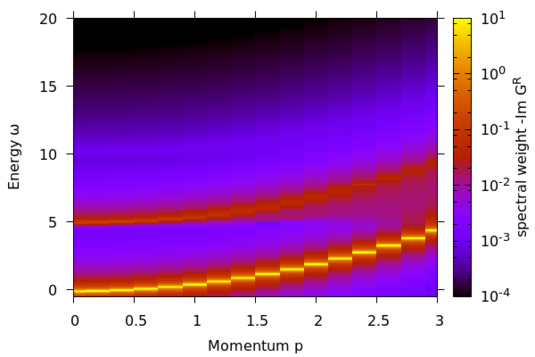 Diagrammatic Monte Carlo is routinely used to sample this diagrammatic series stochastically in imaginary time where the expansion is free of sign problems. The ground-state energy of the polaron has been extracted from the asymptotic behavior of the polaron Green's function in imaginary time. However, to access the excitation spectrum one has to rely on analytic continuation which is numerically ill-posed and prone to spurious spectral features. We aim to bypass the analytic continuation by sampling the diagrammatic series directly in real time (see figure). In order to manage the resulting severe sign (phase) problem, non-crossing diagrams are summed up self-consistently and the resulting bold propagator is used to sample the remaining crossing diagrams more efficiently.
Diagrammatic Monte Carlo is routinely used to sample this diagrammatic series stochastically in imaginary time where the expansion is free of sign problems. The ground-state energy of the polaron has been extracted from the asymptotic behavior of the polaron Green's function in imaginary time. However, to access the excitation spectrum one has to rely on analytic continuation which is numerically ill-posed and prone to spurious spectral features. We aim to bypass the analytic continuation by sampling the diagrammatic series directly in real time (see figure). In order to manage the resulting severe sign (phase) problem, non-crossing diagrams are summed up self-consistently and the resulting bold propagator is used to sample the remaining crossing diagrams more efficiently.

