Foundation of Fermionic Entanglement

Entanglement is one of the most fascinating concepts of modern physics. There are three rather different reasons for the significance of entanglement in various fields in physics and chemistry: (i) It provides important insights into the properties and behaviour of physical and chemical systems. Prime examples are the formation/breaking of chemical bonds and quantum phase transitions, (ii) it serves as a diagnostic tool for the description of many-body quantum states in general. Consequently, its rigorous quantification facilitates the development of more efficient numerical methods for calculating, e.g., ground state energies of strongly interacting many-body quantum systems, (iii) it is an important resource used in the quantum information sciences to realizing quantum information processing tasks.

A lot of effort in quantum information theory has been spent to develop a solid foundation for entanglement between distinguishable systems (“Alice versus Bob”). Yet, given (i) and (ii), the concept of entanglement in systems of identical particles (e.g., electrons) would be even more important. The indistinguishable character of identical fermions leads to a couple of obstacles though. For instance, the concept of entanglement refers to a notion of physical subsystems. But where is a respective tensor product structure in the Hilbert space of N-electron antisymmetrized wave functions? Even if we found one notion of subsystems it is not unique by any means.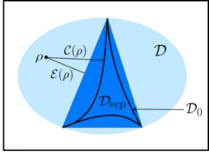                                                                                                                                               
Inspired by “resource theory” we elaborate on the two most natural definitions of fermion entanglement and correlation. The first one describes how close our N-electron state is to the set of particle-uncorrelated “Slater determinant”-states. The second one refers to the 2nd quantization and describes how strongly orbitals (rather than particles) are entangled and correlated. As explained in great detail in [1,2,3] we develop corresponding entanglement and correlation measures by exploiting the common geometric picture of quantum states (see figure). We believe that the concept of such particle and orbital correlation provides a concise and operationally meaningful alternative to the concept of static and dynamic correlations, as used in chemistry and material sciences [1]. Furthermore, we are working on protocols for extracting entanglement from concrete chemical systems. In particular, we are interested in understanding how much work the entanglement extraction requires to overcome the individual binding energies [4].

[1] L.Ding, C.Schilling, J. Chem. Theory Comput. 16, 4159 (2020)

[2] L.Ding, S.Mardazad, S.Das, S.Szalay, U.Schollwöck, Z.Zimborás, C.Schilling, J. Chem. Theory Comput. 17, 1, 79 (2020)

[3] S.Szalay, Z.Zimborás, M.Máté, G.Barcza, C.Schilling, Ö.Legeza, arXiv:2006.03087 (2020)

[4] L.Ding, Z.Zimboras, C.Schilling, forthcoming