Generalized Pauli Constraints
The Pauli exclusion principle is one of the most fundamental laws in physics since it constrains the distribution of electrons in space. It is responsible for the stability of matter with stunning consequences in both the micro and the macro world. However, a recent mathematical breakthrough has shown that the traditional exclusion principle is incomplete and the fermionic exchange symmetry implies further constraints on fermionic occupation numbers. It was one of our main research activities during the past eight years to explore, confirm and quantify the physical relevance of those generalized Pauli constraints (GPCs) in various few-fermion quantum systems. To be more specific, by resorting to both analytical and numerically exact methods we have found that the GPCs are always approximately saturated for ground states [1,2,3,4,5,6,7]. From a geometric point of view this means that the vector of occupation numbers lies very close to the boundary of the allowed region (polytope, see figure). But what is the physical relevance of this phenomenon, which I have introduced as quasipinning? Remarkably, by resorting to mathematical and numerical tools, we have found and eventually proven that (quasi)pinning implies a significantly simplified structure of the corresponding N-fermion quantum state [8,9,10,11]. Moreover, (quasi)pinned systems define new physical entities since their response to external perturbations is rather limited. Based on this robustness, we have proposed in Ref. [12] a transparency effect.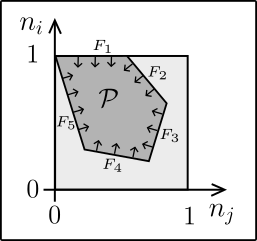 
The presence of approximate pinning (quasipinning) rather than pinning in realistic systems can be seen as a big surprise: What does occupation number vectors in the vicinity of the polytope boundary prevent from lying exactly on the boundary? Just recently, we have discovered the reason for the absence of pinning: The fermionic exchange symmetry manifests itself in the form of an “exchange force” emerging from the different polytope facets preventing the occupation number vector from reaching the boundary (see figure) [13]. It will be one of the crucial challenges for the nearer future to experimentally visualize this exchange force and to understand its consequences for the development of functional theories. Moreover, since (quasi)pinning corresponds to specific simplified N-fermion quantum states, we are developing a hierarchy of generalized Hartree-Fock ansatzes which would allow one to recover in a systematic way step-by-step the most important N-electron configurations contributing to the ground state of molecular systems [14,10].
[1] C.Schilling, D.Gross, M.Christandl, Phys. Rev. Lett. 110, 040404 (2013)
[2] C.Schilling, Phys. Rev. B 92, 155149 (2015)
[3] F.Tennie, D.Ebler, V.Vedral, C.Schilling, Phys. Rev. A 93, 042126 (2016)
[4] F.Tennie, V.Vedral, C.Schilling, Phys. Rev. A 94, 012120 (2016)
[5] F.Tennie, V.Vedral, C.Schilling, Phys. Rev. A 95, 022336 (2017)
[6] C.Schilling, M.Altunbulak, S.Knecht, A.Lopes, J.Whitfield, M.Christandl, D.Gross, M.Reiher, Phys. Rev. A 97, 052503 (2018)
[7] Ö.Legeza, C.Schilling, Phys. Rev. A 97, 052105 (2018)
[8] C.Schilling, Phys. Rev. A 91, 022105 (2015)
[9] C.Schilling, C.Benavides-Riveros, P.Vrana, Phys. Rev. A 96, 052312 (2017)
[10] C.Schilling, C.Benavides-Riveros, A.Lopes, T.Maciążek, A.Sawicki, New J. Phys. 22, 023001 (2020)
[11] T.Maciążek, A.Sawicki, D.Gross, A.Lopes, C.Schilling, New J. Phys. 22, 023002 (2020)
[12] C.Schilling, Phys. Rev. B 92, 155149 (2015) [13] C.Schilling, R.Schilling, Phys. Rev. Lett. 122, 013001 (2019)
[14] C.Benavides-Riveros, C.Schilling, Z. Phys. Chem. 230, 703 (2016)