Reduced Density Matrix Functional Theory
Density functional theory (DFT) is the workhorse of modern electronic structure calculations in physics, chemistry and material sciences. Its popularity is mainly based on its low computational cost with a scope even covering macroscopically large systems. Yet, DFT has several fundamental limitations in its present form. The most prominent one is its inability to deal with strongly correlated systems, particularly those dominated by static correlations. That’s not surprising since its implementation according to Kohn-Sham establishes a natural relation between the density and a single Slater determinant. To describe strongly correlated systems in a more natural way, it has been suggested to upgrade DFT by involving the full 1-particle reduced density matrix (1RDM) rather than just the spatial density. Allowing explicitly for fractional occupation numbers, the corresponding 1RDMFT has proven to be much more suitable for the description of strongly correlated systems. 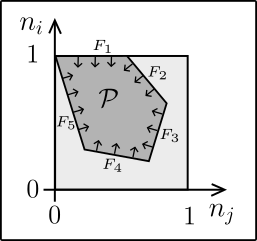 One of our main goals is to establish a solid foundation for 1RDMFT. By using concise tools from quantum information theory and mathematical physics we are deriving universal features of the unknown exact 1RDM-functional. For instance, a general relation between 1RDMs and the corresponding N-fermion quantum states [1,2] allowed us to prove that the gradient of the universal functional diverges repulsively whenever fermionic occupation numbers n attain the minimal or maximal values, n=0,1 [3]. In other words, we succeeded in proving that the fermionic exchange symmetry manifests itself in all fermionic quantum systems in the form of a diverging “exchange force” (see figure). Application of RDMFT to bosonic quantum systems leads to a similar feature, a so-called Bose-Einstein force [4,5]. This new concept provides a concise and universal explanation for the absence of BEC of full degree in nature (“quantum depletion”).
One of our main goals is to establish a solid foundation for 1RDMFT. By using concise tools from quantum information theory and mathematical physics we are deriving universal features of the unknown exact 1RDM-functional. For instance, a general relation between 1RDMs and the corresponding N-fermion quantum states [1,2] allowed us to prove that the gradient of the universal functional diverges repulsively whenever fermionic occupation numbers n attain the minimal or maximal values, n=0,1 [3]. In other words, we succeeded in proving that the fermionic exchange symmetry manifests itself in all fermionic quantum systems in the form of a diverging “exchange force” (see figure). Application of RDMFT to bosonic quantum systems leads to a similar feature, a so-called Bose-Einstein force [4,5]. This new concept provides a concise and universal explanation for the absence of BEC of full degree in nature (“quantum depletion”).
Another crucial challenge is to understand how the generalized Pauli constraints (GPCs) enter RDMFT. In a first analytical work, we provided strong evidence that the role of the GPCs has been underestimated in RDMFT so far and that they might significantly shape the form of the universal functional [6].
In the context of solid state physics, RDMFT simplifies significantly. For instance for translationally invariant 1-band lattice models, the natural orbitals are known from the very beginning and RDMFT reduces de facto to a momentum occupation number-functional theory. In that context we proposed recently a scheme for developing a hierarchy of functional approximations by referring to different orders of irreducible fermionic particle entanglement [3]. It is one of our ambitions to work out and test the corresponding approximations, particularly for strongly correlated systems (e.g., 2d Hubbard models).
Last but not least, by resorting to a generalization of the Rayleigh-Ritz variational principle to mixed states we proposed and worked out an RDMFT for targeting the energies of selected excited states [7-9]. These works also highlight the excellent prospects that tools from convex analysis provide for advancing functional theories. In particular, they alllowed us to solve an underlying one-body N-reprsentability problem and accordingly we discovered a remarkable generalization of Pauli's famous exclusion principle to bosons and fermionic excited states [10]. It is one of our ongoing research endeavours to understand the general physical relevance of those exclusion principles and to derive first functional approxiimations for calculating excitation energies.
[1] C.Schilling, Phys. Rev. A 91, 022105 (2015)
[2] C.Schilling, C.Benavides-Riveros, P.Vrana, Phys. Rev. A 96, 052312 (2017)
[3] C.Schilling, R.Schilling, Phys. Rev. Lett. 122, 013001 (2019)
[4] C.Benavides-Riveros, J.Wolff, M.Marques, C. Schilling, Phys. Rev. Lett. 124, 180603 (2020)
[5] J.Liebert, C.Schilling, Phys. Rev. Research 3, 013282 (2021)
[6] C.Schilling, J. Chem. Phys. 149, 231102 (2018)
[7] C.Schilling, S.Pittalis, Phys. Rev. Lett. 127, 023001 (2021)
[8] J.Liebert, F.Castillo, J.-P.Labbé, C.Schilling, J. Chem. Theory Comput. 2022, 18, 124 (2022)
[9] J.Liebert, C.Schilling, arXiv:2204.12715
[10] F.Castillo, J.-P.Labbé, J.Liebert, A.Padrol, E.Philippe, C.Schilling, arXiv:2105.06459

