Phase-Space Geometry of Mass-Conserving Reaction-Diffusion Dynamics
Fridtjof Brauns, Jacob Halatek, Erwin Frey
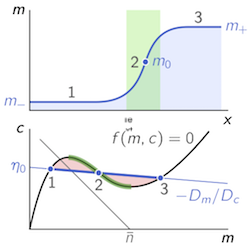In this study, we present a novel theoretical framework that extends the geometric concepts underlying the analysis of nonlinear ODEs to spatially extended, pattern-forming, non-equilibrium systems, as described by reaction-diffusion equations.
In recent years, experimental studies of protein pattern formation (both in vivo and in vitro) have sparked new interest in the dynamics of reaction–diffusion systems. Yet, general theories for reaction–diffusion systems have remained limited to the linear regime in the vicinity of homogeneous steady states, where the system’s dynamical properties can be extracted from the Jacobian (linearization of the dynamics around the homogeneous steady state). In general, the strongly nonlinear dynamics of pattern formation far from the homogeneous steady state remains inaccessible to this approach and has been amenable to numerical investigation only. Therefore, a comprehensive theory for pattern formation beyond the linear regime is still missing.
Here, we present the foundations of a novel theoretical framework for reaction-diffusion systems with conserved quantities. Our approach is inspired by the geometric analysis of nonlinear ODE systems, where key insights into the system’s dynamics can be gained from its phase-space structure. From a mathematical point of view, one would expect any attempt to generalize the phase-space analysis to spatially extended PDE systems to be a futile exercise, given that PDE phase spaces are infinite-dimensional and that the geometric analysis is feasible only for lower-dimensional ODE phase spaces. Instead of focusing on the pure mathematical problem, we aimed to decompose the dynamics into the key physical processes driving pattern formation: reaction and diffusion. Specifically, we were able to unambiguously embed the action of diffusive coupling within the low-dimensional phase space of the reaction kinetics. This major insight enabled us to develop a broad repertoire of methods for tackling the entire time evolution of pattern-forming processes in complete analogy to the traditional phase-space analysis of ODEs.
We are particularly excited by the fact that this approach reveals the general physical principle underlying self-organized pattern formation in mass-conserved reaction-diffusion systems: the mass-redistribution cascade.
As a conserved quantity, the system’s mass defines the equilibria of the dynamics. Local changes in mass shift the local chemical equilibria, and thereby induce concentration gradients. These gradients, in turn, lead to diffusive redistribution of mass, and therefore to further shifting of the local chemical equilibria. We find that these principles are unambiguously encoded in simple geometric structures within the reactive phase space: The kinetic nullcline determines how local equilibria shift due to mass redistribution; the flux-balance subspace determines how diffusive coupling redistributes mass which results in a patterned steady state. Strikingly, this flux-balance principle can be interpreted as a non-equilibrium generalization of the chemical potential and reveals a direct connection to the common tangent construction employed to find the coexisting phases of a phase-separated binary mixture near thermal equilibrium.
The theory we present enables the traditional separation between linear and nonlinear regimes to be overcome: The effect of nonlinearities on the global pattern-formation dynamics is simply encoded in the shape of the line of chemical equilibria in phase space (the reactive nullcline). This major advantage opens completely new ways to analyze pattern-forming reaction-diffusion systems. In particular, we show that the cornerstones of nonlinear dynamics are all recoverable as geometric properties of the phase-space structure, including linear instability and excitability, as well as the characteristics and bifurcations of patterns. We find simple geometric conditions for both lateral instability (“Turing instability”) and excitability (“nucleation threshold”). Most significantly, the central entities in our theory, chemical equilibria, are accessible to experimental determination. This allows one to quantify by experiment many of the fundamental features of self-organization predicted by our theory.
Since the fundamental elements of our framework, conserved quantities that control local interactions, underlie many non-equilibrium systems, our framework straightforwardly lends itself to various directions of generalization. Starting from three-component reaction-diffusion systems, one can proceed to systems with even more components and conserved quantities, and ultimately to active matter and granular media.