Anomalous collective dynamics of autochemotactic populations
Jasper van der Kolk, Florian Rasshofer, Richard Swiderski, Astik Haldar, Abhik Basu, and Erwin Frey
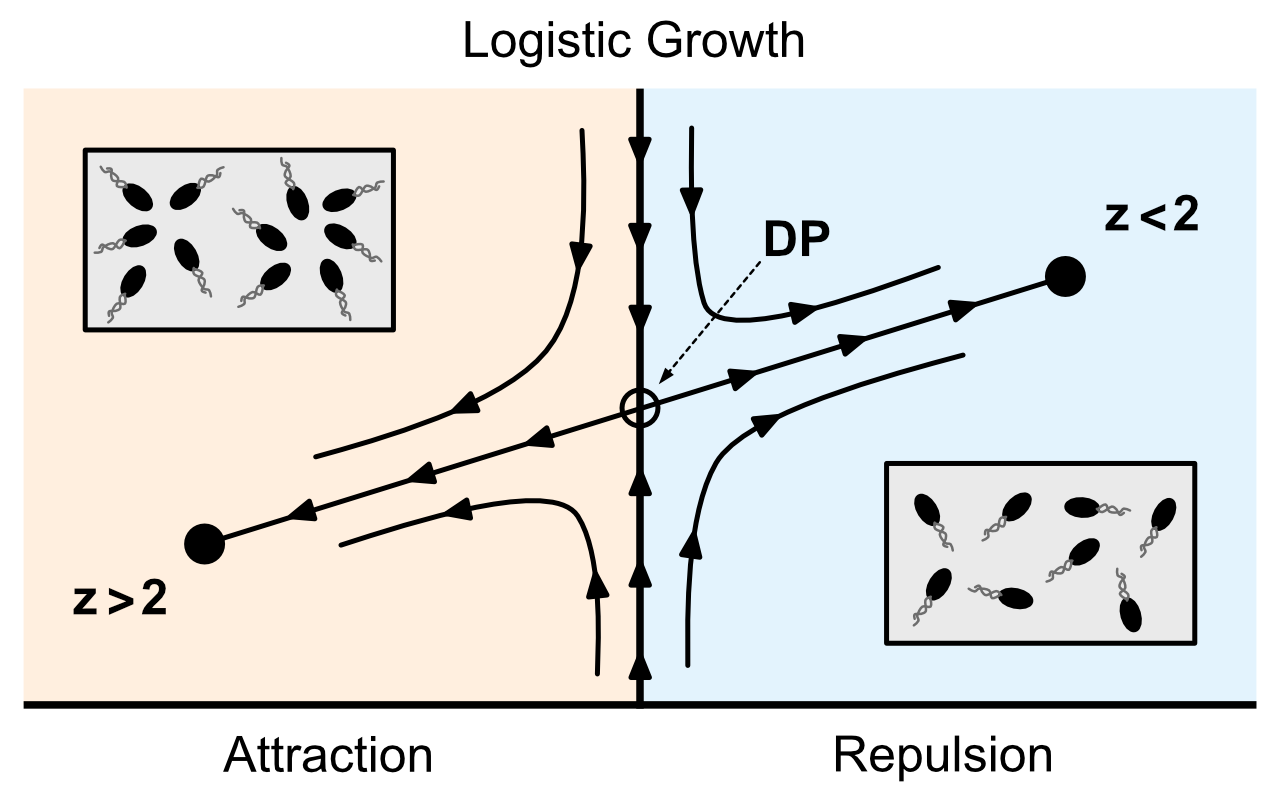 In studies of nonequilibrium phase transitions, many different forms of local interactions have been investigated. But how do long-ranged interactions influence the critical dynamics of a colony of active agents? In order to study this question, we analyze the critical dynamics of reproducing agents subject to long-range chemical interactions and limited resources. Specifically, we study a model of chemically interacting agents, whose population dynamics are accounted for by Fisher-Kolmogorov dynamics. The chemotactic interaction is modeled by Keller-Segel like active motion, i.e., the agents are assumed to preferably move along gradients in a chemical field sourced by themselves.
In studies of nonequilibrium phase transitions, many different forms of local interactions have been investigated. But how do long-ranged interactions influence the critical dynamics of a colony of active agents? In order to study this question, we analyze the critical dynamics of reproducing agents subject to long-range chemical interactions and limited resources. Specifically, we study a model of chemically interacting agents, whose population dynamics are accounted for by Fisher-Kolmogorov dynamics. The chemotactic interaction is modeled by Keller-Segel like active motion, i.e., the agents are assumed to preferably move along gradients in a chemical field sourced by themselves.
By means of a renormalization group analysis of the full stochastic model we discover novel subdiffusive (superdiffusive) scaling regimes for instantaneous attractive (repulsive) interactions. In contrast, for slow signal transduction, we find that the dynamics are controlled by a purely diffusive fixed point with a surprising similarity to the critical fixed point of the Kardar-Parisi-Zhang equation – an indication of possible strong coupling behavior. This strongly emphasizes the importance of the speed of chemical signal transduction which has been underestimated in previous studies. We also present a novel nonlinear mechanism that stabilizes the continuous transition against the emergence of a characteristic length scale due to chemotactic collapse.
Thus, our results suggest that new interesting universal behavior can be observed by combining known universality classes of nonequilibrium population dynamics with long-ranged interactions (for example different kinds of chemotactic interactions).

