Noise and Correlations in a Spatial Population Model with Cyclic Competition
Tobias Reichenbach, Mauro Mobilia and Erwin Frey
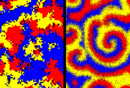
Noise and spatial degrees of freedom characterize pattern formation in biological systems. As an example, laboratory experiments on microbial communities have shown that different bacterial strains on Petri dishes self-organize into irregular clusters if bacteria are static [Nature 418, 171-174 (2002)].
However, the theoretical description of such noisy, out-of-equilibrium patterns constitutes considerable challenges. Here, we devise an analytic approach that is generally applicable when individuals are mobile. Recently, we have shown that mobility has crucial impact on the maintenance of biodiversity in ecological systems [Nature 448, 1046-1049 (2007)] [arXiv:0709.0217].
Here, we explore the influence of mobility on pattern formation properties. Within a prototypical model of three interacting species, we find that mobility renders the emerging spatial structures surprisingly regular; in our case, an entanglement of rotating spiral waves forms. We discuss the cases of low and high mobility, and present an analytical framework for the high-mobility scenario in the form of stochastic partial differential equations and an underlying complex Ginzburg-Landau equation. This approach allows for intriguing insights into the role of mobility and noise on self-organizing patterns.