Statistical Physics
The theory of equilibrium phase transitions and critical phenomena has enjoyed tremendous success in the past decades. Scaling concepts and renormalization group ideas have led to both qualitative and quantitative understanding of the fundamental physics involved, and to quantitative explanations of experiments on a very broad range of materials and substances. In contrast, scaling properties and phase transitions in systems far from equilibrium are as yet comparatively poorly understood. Understanding systems out of equilibrium is still among one of the most challenging problems in theoretical physics. Actually, many if not most natural processes are out of equilibrium. Soft materials are often versatile model systems to study fundamental questions in non-equilibrium physics.
Our goal is to identify to governing principles and control parameters of collective fluctuations and complex spatio-temporal patterns far from equilibrium. We would like to focus on the influence of anisotropies, correlations in the stochastic driving forces, long-ranged interactions and coupled degrees of freedom on the collective dynamics. This requires to unravel the subtle interplay between diffusion, convection and feedback between various degrees of freedom. The topics of these studies will mainly be problems from surface growth, the dynamics of elastic manifolds in disordered and structured media, colloidal suspensions and glass forming systems.
Current Research
-
We are honored to announce the 32nd Arnold Sommerfeld Lecture Series featuring Professor Mehran Kardar (MIT), a pioneer in statistical physics and recipient of the 2025 Boltzmann Medal. Taking place January 13–15, 2026, the series begins with a public lecture on the mysterious "Force of Nothing" in the quantum void, followed by expert talks on active matter and biological population dynamics. Join us for this exciting exploration of non-equilibrium systems and fluctuation phenomena.
more
-
Absorbing state phase transitions are an important class of stochastic systems which are
of fundamental importance for the field on nonequilibrium and statistical physics, while
being directly or conceptually relevant to a variety of natural processes. The diffusive
epidemic process (DEP) is a paradigmatic model in this class, introduced as a minimal
model for the stochastic spreading of an epidemic. Unlike directional percolation, the
process involves two different types of individuals/particles (healthy and diseased
individuals) that diffuse with different diffusion constants and where the total number of
individuals is conserved. Interestingly, it has also been discussed as a minimal model for
the emergence of protein pattern in cell polarity systems.
more
-
Our work on topological phases in biology was recently highlighted in Physics Today. Topological effects are increasingly being studied in systems outside of hard condensed matter physics -- for example, in fluids composed of self-propelled particles, and in some atmospheric and ocean waves. Our group has identified topological phases in an ecological model. The work points to the potential application of topology to other dynamical biological systems.
more
-
In modern research, a new class of gaseous systems, so-called active gases arouses the interest of many scientists. Unlike gas molecules at thermal equilibrium, the constituent particles of active gases are self-propelled, and mutual interactions are typically highly dissipative. Such systems are far from thermal equilibrium and exhibit a wealth of patterns on macroscopic scales, which ultimately arise as a consequence of activity and dissipation at the microscopic level. Its distinctive capabilities to mediate between the microscopic and macroscopic views on physical systems therefore makes the Boltzmann equation a conceptually highly appealing tool in understanding the unusual collective dynamics of such active systems.
more
-
In this letter we study how topological defects affect the degree of polar and crystalline order in active matter at high densities. To this end, we analyze a generic agent-based model, which accounts for both polar alignment and shorted-ranged repulsive interaction.
We show that, while defects still play a decisive role, the emerging defect dynamics and phase behavior differ qualitatively from their equilibrium analogues. In active systems, the non-equilibrium steady states include different types of polycrystalline phases, and an intriguing crystalline phase with quasi-long-range translational order but completely devoid of any topological defects. Moreover, we find that absence of defects and polar order are mutually exclusive features. When alignment forces dominate over repulsive forces, polar states are favored. The resulting collective particle flux makes the system highly susceptible to the spontaneous formation of grain boundaries and thereby repeatedly creates small crystalline patches. These spontaneous fracture-like processes are accompanied by propagating sound waves. In contrast, in systems with strong repulsive forces the formation of a crystalline state precludes the formation of collectively moving
clusters. Surprisingly, the phonon modes in this active crystalline state lead to quasi-long-range order but the fluctuations generated by the active particle motion do not create topological defects.
more
-
In recent years, kinetic theory has gained considerable popularity to asses the large scale properties of self-propelled particle (SPP) systems. Specifically, the Boltzmann equation provides a compelling link between a microscopic, particle-level description of active systems, and the corresponding set of macroscopic equations. Yet, the applicability of Boltzmann's equation in the context of active media, as well its limitations due to the molecular chaos assumption remain largely elusive.
more
-
The emergence of collective motion in fish schools and bird flocks constitutes a ubiquitous and fascinating phenomenon in nature. One reason might be the emergence of highly dynamic, coherently moving spatial patterns such as clusters, swirls or waves, and the fact that the patterns commonly extend over length scales much larger than the size of the individuals.
more
-
The law of mass action describes the speed of chemical reactions. Our model calculations demonstrate, however, that at sufficiently high reactant densities the law is violated. The deviations are attributed to many-particle effects.
more
-
Dense liquids of infinitely thin, hard needles challenge Statistical
Mechanics: while its equilibrium properties correspond to those of an
ideal gas, the steric hindrance of the needles induces complex dynamic
behavior. An intriguing phenomenon is the enhancement of translational
diffusion over several orders of magnitude as density increases. Such a
behavior contradicts the experience that transport becomes slow in dense
complex liquids. We observed the emergence of a spacious zigzag motion of
the needle, which results in a power-law increase of the
diffusion coefficient with the mysterious exponent 0.8.
more
-
Conformational transitions in macromolecular complexes often involve the reorientation of lever-like structures. Using a simple theoretical model, we show that the rate of such transitions is drastically enhanced if the lever is bendable, e.g. at a localized "hinge". Surprisingly, the transition is fastest with an intermediate flexibility of the hinge. In this intermediate regime, the transition rate is also least sensitive to the amount of "cargo" attached to the lever arm, which could be exploited by molecular motors. To explain this effect, we generalize the Kramers-Langer theory for multi-dimensional barrier crossing to configuration dependent mobility matrices.
more
-
Spatial heterogeneities often give rise to intriguing slow dynamics in complex materials, manifested for example by broad frequency-dependent relaxation processes in colloidal gels which form stress-sustaining networks close to the sol-gel transition. A further prominent example are sodium silicates, where the formation of a space-filling network of channels allows for slow diffusion of sodium ions in an arrested host matrix. A minimal model that encompasses spatial disorder and slow dynamics is provided by the Lorentz model, i.e., classical point particles explore without mutual interaction a d-dimensional space in the presence of a frozen array of randomly distributed (possibly overlapping) hard spherical obstacles.
more
-
With help of a light microscope one can see single chromosomes, the closest packed form of DNA. Not only during cell division, but throughout the whole cell cycle, DNA in eucaryotes is packed in one way or another. On the smallest scale, DNA is wrapped around histones and forms nucleosomes. The readout of information - between cell divisions - is controlled by so called transcription factors, which can bind to DNA without ATP consumption. How can that be if DNA is packed?
more
-
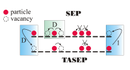
Driven diffusive lattice gases have not only been frequently used to model biological transport by molecular motors, but serve also to investigate the intriguing problems of non-equilibrium physics. Two such systems are the total asymmetric exclusion process (TASEP) and the symmetric exclusion process (SEP) that can be regarded as the simplest paradigms of driven (TASEP) and diffusive (SEP) transport.
more
-
Cars jamming in city centers or on highways belong to our every-day experience. In the present work, we theoretically explore such traffic phenomena occurring at a much smaller size, on the nanometer scale. At these tiny lengths, the fields of biological physics and information technology become increasingly intertwined. Still, different paradigms rule in these areas. Brownian motion governs biological systems, e.g., it drives molecular motors along parallel one-dimensional filaments in cells, serving as transport engines. On the other hand, quantum effects become visible in the field of electronic information processing.
more
-
Nature as well as modern technology presents us a variety of disordered materials ranging from composites over gels to the inner structure of biological cells. We have shown that the transport properties of microscopic particles in such materials are directly connected to strong structural heterogeneities resulting from the presence of a broad range of length scales. It is known that these heterogeneities lead to a dramatic slowing down of transport processes due to a fractal dynamic behavior which has to be contrasted to normal diffusion. The latter being tightly bound to Brownian motion, is the dominant transport process in homogeneous materials and can be characterized by single length and time scales. Heterogeneous materials, however, lack such a single length scale, and the new fractal transport law depends on non-integer, i.e. fractal, powers of time and length.
more
-
Superimposing optical interference patterns to two-dimensional colloidal systems generates versatile soft matter systems which allow to study the subtle interplay between thermal fluctuations, intermolecular interactions and external potentials on the ordering of the colloidal particles. These systems serve as model systems to study hard matter physics: the interfering laser patterns mimic the substrate potential of a crystalline surface and the assemblies of colloidal particles in the potential minima mimic molecules of various symmetries. Depending on the strength of the fluctuations, the symmetry of the laser patterns and the soft colloidal molecules novel phases emerge.
more