· Strongly Correlated Quantum Systems
· Advanced Numerical Methods
· Quantum Matter

Dynamical Scaling and Planckian Dissipation due to Heavy-Fermion Quantum Criticality (Editor’s Suggestion)
Phys. Rev. Lett. 134, 106501 (2025), A. Gleis, S.-S. B. Lee, G. Kotliar, and J. von Delft

We study heavy-fermion quantum criticality in the periodic Anderson model, finding a strange-metal regime emerging from a Kondo-breakdown quantum critical point. There, the optical conductivity shows dynamical scaling behavior with exponents equal to those observed in experiments. In stark contrast to the Yukawa-SYK approach, the strange metal is intrinsic (i.e., disorder-free) and arises from qualitatively important vertex contributions encoding non-perturbative two-particle scattering. Our work takes an essential step towards understanding strange metals without invoking the marginal Fermi liquid paradigm (e.g., SYK approaches).

Emergent Properties of the Periodic Anderson Model: A High-Resolution, Real-Frequency Study of Heavy-Fermion Quantum Criticality
Phys. Rev. X 14, 41036 (2024), A. Gleis, S.-S. B. Lee, G. Kotliar, J. von Delft

Heavy Fermion metals are usually alloys containing rare earth elements with partially filled, highly localized f orbitals. At low temperatures, coherent tunneling between f orbitals and itinerant conduction bands usually leads to effective delocalization of the f electrons, a phenomenon known as lattice Kondo effect. About 30 years ago, quantum phase transitions featuring a sudden localization of the f electrons were discovered. Subsequent work showed that such “Kondo breakdown” transitions are often accompanied by phenomena like unconventional superconductivity and strange metal behavior. These experimental developments raised fundamental questions that still await detailed answers. Does the localization of f electrons require the complete suppression of tunneling between f orbitals and conduction bands at low energies? How does strange-metal behavior emerge in the vicinity of
the Kondo breakdown? Here, we perform an in-depth study of a Kondo breakdown transition, using theoretical methods yielding unprecedented access to low-energy properties. We conclude, in contrast to previous studies, that a complete suppression of low-energy tunneling between conduction bands and f orbitals is not necessary to localize f electrons. We rather find that the localization is driven by the emergence of a so-called Luttinger surface, a set of disallowed momenta for the f electrons at low energies. Further, we find a novel stable quantum critical point with intrinsic strange-metal-like properties. Our work provides improved understanding of the Kondo breakdown phenomenon and a new route to understanding strange metallicity.

Time-Dependent Variational Principle with Controlled Bond Expansion for Matrix Product States
Phys. Rev. Lett. 133, 26401 (2024), J.-W. Li, A. Gleis, and J. von Delft

We present a controlled bond expansion (CBE) approach to simulate quantum dynamics based on the time-dependent variational principle (TDVP) for matrix product states (MPS). CBE resolves the numerical difficulty of the standard TDVP method for MPS, where dominant projection errors spoil the numerical accuracy.Our results show that CBE--TDVP can achieve high (2-site) accuracy at low (1-site) costs, and require only minor modifications of standard MPS--TDVP implementations.
CBE--TDVP thus opens new possibilities for MPSs to simulate large-scale dynamics of complex quantum systems. This is of great interest to tensor network practitioners, strongly correlated physics and quantum chemistry communities.

Quantics Tensor Cross Interpolation for High-Resolution, Parsimonious Representations of Multivariate Functions in Physics and Be
Phys. Rev. Lett. 132, 056501 (2024), M. K. Ritter, Y. N. Fernandez M. Wallerberger, J. von Delft,H. Shinaoka, X. Waintal

Multivariate functions of continuous variables arise in countless branches of science. Numerical computations with such functions typically involve a compromise between two contrary desiderata: accurate resolution of the functional dependence, versus parsimonious memory usage. Recently, two promising strategies have emerged for satisfying both requirements: (i) The quantics representation, which expresses functions as multi-index tensors, with each index representing one bit of a binary encoding of one of the variables; and (ii) tensor cross interpolation (TCI), which, if applicable, yields parsimonious interpolations for multi-index tensors. Here, we present a strategy, quantics TCI (QTCI), which combines the advantages of both schemes. We illustrate its potential with an application from condensed matter physics: the computation of Brillouin zone integrals.

Symmetric improved estimators for multipoint vertex functions
Phys. Rev. B 109, 125138 (2024), J.-M. Lihm, J. Halbinger, J. Shim, J. von Delft, F. B. Kugler, S.-S. B. Lee

The two-particle vertex is a key quantity in quantum many-body physics, which describes how the effective interaction between particles depends on the particles’ energies. However, due to its complicated frequency dependence and many potential sources of numerical errors, the accurate calculation of the vertex, especially for strong interactions and low temperatures, remains extremely challenging. Here, we develop a new representation of vertex functions, “symmetric improved estimators,” that improve the accuracy and stability of their calculations. The estimators naturally decompose a vertex into the sum of terms with different characteristic behaviors and large-frequency limits. As each term is evaluated separately, one thereby accurately resolves the multifaceted frequency dependence.
We use our method, in combination with the multipoint numerical renormalization group, to calculate the two-particle vertex of the Anderson impurity model, a prototypical many-body Hamiltonian. We demonstrate that using symmetric improved estimators drastically improves the quality of the vertex compared to using the asymmetric improved estimator. The accuracy of the vertex is demonstrated by multiple stringent tests, such as the agreement with perturbation theory in the weak-coupling regime, with Fermi-liquid theory at energy scales below the Kondo temperature, and with general fluctuation-dissipation relations.
Our finding opens the way for studying electronic correlation in systems or parameter regimes that had previously been beyond computational reach.

Real-frequency quantum field theory applied to the single-impurity Anderson model
Phys. Rev. B 109, 115128 (2024)(1995), A. Ge, N. Ritz, E. Walter, S. Aguirre, J. v. Delft, F. B. Kugler

p>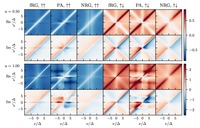A major challenge in the field of correlated electrons is the computation of dynamical correlation functions. For comparisons with experiment, one is interested in their real-frequency dependence. This is difficult to compute, as imaginary-frequency data from the Matsubara formalism require analytic continuation, a numerically ill-posed problem. Here, we apply quantum field theory to the single-impurity Anderson model (AM), using the Keldysh instead of the Matsubara formalism with direct access to the self-energy and dynamical susceptibilities on the real-frequency axis. We presentresults from the functional renormalization group (fRG) at one-loop level and from solving the selfconsistent parquet equations in the parquet approximation. In contrast to previous Keldysh fRG works, we employ a parametrization of the four-point vertex which captures its full dependence on three real-frequency arguments. We compare our results to benchmark data obtained with the numerical renormalization group and to second-order perturbation theory. We find that capturing the full frequency dependence of the four-point vertex significantly improves the fRG results compared to previous implementations, and that solving the parquet equations yields the best agreement with the NRG benchmark data, but is only feasible up to moderate interaction strengths. Our methodical advances pave the way for treating more complicated models in the future.

Controlled Bond Expansion for Density Matrix Renormalization Group Ground State Search at Single-Site Costs
Phys. Rev. Lett. 130, 246402 (2023), A. Gleis, J.-W. Li, and J. von Delft

We present a new tensor network technique, controlled bond expansion (CBE), for expanding virtual bonds and apply it to the density matrix renormalization group (DMRG) for ground-state search. CBE resolves the issue of DMRG requiring either an expensive 2-site update or non-variational mixing parameters. Our results show that CBE-DMRG provides high accuracy at low (1-site) cost, requiring minor modifications to existing codes. CBE opens up new possibilities to improve the efficiency of tensor network techniques, with CBE--DMRG providing an example of its usefulness. Our findings are of great interest for the tensor network, correlated many-body and quantum chemistry communities.

Projective symmetry group classification of chiral Z2 spin liquids on the pyrochlore lattice: Application to the spin-1/2 XXZ Heisenberg model
Phys. Rev. B 105, 125122 (2022), B. Schneider, J. C. Halimeh, M. Punk

Simplified models for quantum spin-ice materials, such as the XXZ model on the pyrochlore lattice, may host interesting new spin-liquid ground states. In this work, we provide a complete classification of nearest-neighbor chiral Z2 spin-liquid states on the pyrochlore lattice using a projective symmetry group analysis. Moreover, the newly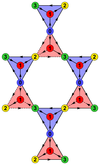

states are applied to the XXZ model within a self-consistent mean-field scheme. We find a new class of spin-liquid states, the pi/3-states, that inherit their properties from fractionalization of the C3 symmetry of the pyrochlore lattice. Further, we discuss observable signatures that can be measured in neutron scattering experiments. Remarkably, the spin liquids preserve the SU(2) symmetry even in the presence of SU(2) symmetry breaking interactions.

 

 

Multipoint Correlation Functions: Spectral Representation and Numerical Evaluation &
Computing Local Multipoint Correlators Using the Numerical Renormalization Group
Phys. Rev. X 11, 041007 (2021), S.-S. B. Lee ,F. B. Kugler, J. von Delft

Local three- and four-point correlators yield important insight into strongly correlated systems and have many applications. However, the nonperturbative, accurate computation of multipoint correlators is challenging, particularly in the real-frequency domain for systems at low temperatures. In the accompanying paper, we introduce generalized spectral representations for multipoint correlators. Here, we develop a numerical renormalization group approach, capable of efficiently evaluating these spectral representations, to compute local three- and four-point correlators of quantum impurity models. The key objects in our scheme are partial spectral functions, encoding the system’s dynamical information. Their computation via numerical renormalization group allows us to simultaneously resolve various multiparticle excitations down to the lowest energies. By subsequently convolving the partial spectral functions with appropriate kernels, we obtain multipoint correlators in the imaginary-frequency Matsubara, the real-frequency zero-temperature, and the real-frequency Keldysh formalisms. We present exemplary results for the connected four-point correlators of the Anderson impurity model, and for resonant inelastic x-ray scattering spectra of related impurity models. Our method can treat temperatures and frequencies—imaginary or real—of all magnitudes, from large to arbitrarily small ones.

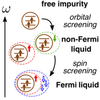
Uncovering Non-Fermi-Liquid Behavior in Hund Metals: Conformal Field Theory Analysis of an SU(2)×SU(3) Spin-Orbital Kondo Model, Phys. Rev. X 10, 031052 (2020), E. Walter, K. M. Stadler, S.-S. B. Lee, Y. Wang, G. Kotliar, A. Weichselbaum, J. von Delft

Hund metals have attracted attention in recent years due to their unconventional superconductivity, which supposedly originates from non-Fermi-liquid (NFL) properties of the normal state. When studying Hund metals using dynamical mean-field theory (DMFT), one arrives at a self-consistent "Hund impurity problem" involving a multiorbital quantum impurity with nonzero Hund coupling interacting with a metallic bath. If its spin and orbital degrees of freedom are screened at different energy scales, the intermediate energy window is governed by a novel NFL fixed point, whose nature had not yet been clarified. We resolve this problem by providing an analytical solution of a paradigmatic example of a Hund impurity problem, involving two spin and three orbital degrees of freedom. To this end, we combine a state-of-the-art implementation of the numerical renormalization group, capable of exploiting non-Abelian symmetries, with a generalization of Affleck and Ludwig’s conformal field theory (CFT) approach for multichannel Kondo models.