Theoretical Solid State Physics
Our group focuses on the study of strongly correlated many particle systems, where interactions play an important role. To do so we use and develop advanced theoretical tools, in particular tensor network and functional renormalization group methods.
Current research highlights
Symmetric improved estimators for multipoint vertex functions
Phys. Rev. B 109, 125138 (2024), J.-M. Lihm, J. Halbinger, J. Shim, J. von Delft, F. B. Kugler, S.-S. B. Lee
The two-particle vertex is a key quantity in quantum many-body physics, which describes how the effective interaction between particles depends on the particles’ energies. However, due to its complicated frequency dependence and many potential sources of numerical errors, the accurate calculation of the vertex, especially for strong interactions and low temperatures, remains extremely challenging. Here, we develop a new representation of vertex functions, “symmetric improved estimators,” that improve the accuracy and stability of their calculations.
classifie d The estimators naturally decompose a vertex into the sum of terms with different characteristic behaviors and large-frequency limits. As each term is evaluated separately, one thereby accurately resolves the multifaceted frequency dependence.
d The estimators naturally decompose a vertex into the sum of terms with different characteristic behaviors and large-frequency limits. As each term is evaluated separately, one thereby accurately resolves the multifaceted frequency dependence.
We use our method, in combination with the multipoint numerical renormalization group, to calculate the two-particle vertex of the Anderson impurity model, a prototypical many-body Hamiltonian. We demonstrate that using symmetric improved estimators drastically improves the quality of the vertex compared to using the asymmetric improved estimator. The accuracy of the vertex is demonstrated by multiple stringent tests, such as the agreement with perturbation theory in the weak-coupling regime, with Fermi-liquid theory at energy scales below the Kondo temperature, and with general fluctuation-dissipation relations.
Our finding opens the way for studying electronic correlation in systems or parameter regimes that had previously been beyond computational reach.
Real-frequency quantum field theory applied to the single-impurity Anderson model
Phys. Rev. B 109, 115128 (2024)(1995), A. Ge, N. Ritz, E. Walter, S. Aguirre, J. v. Delft, F. B. Kugler
A major challenge in the field of correlated electrons is the computation of dynamical correlation functions. For comparisons with experiment, one is interested in their real-frequency dependence. This is difficult to compute, as imaginary-frequency data from the Matsubara formalism require analytic continuation, a numerically ill-posed problem. Here, we apply quantum field theory to the single-impurity Anderson model (AM), using the Keldysh instead of the Matsubara formalism with direct access to the self-energy and dynamical susceptibilities on the real-frequency axis. We presentresults from the functional renormalization group (fRG) at one-loop level and from solving the selfconsistent parquet equations in the parquet approximation. In contrast to previous Keldysh fRG works, we employ a parametrization of the four-point vertex which captures its full dependence on three real-frequency arguments.
classifie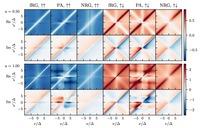 d We compare our results to benchmark data obtained with the numerical renormalization group and to second-order perturbation theory. We find that capturing the full frequency dependence of the four-point vertex significantly improves the fRG results compared to previous implementations, and that solving the parquet equations yields the best agreement with the NRG benchmark data, but is only feasible up to moderate interaction strengths. Our methodical advances pave the way for treating more complicated models in the future.
d We compare our results to benchmark data obtained with the numerical renormalization group and to second-order perturbation theory. We find that capturing the full frequency dependence of the four-point vertex significantly improves the fRG results compared to previous implementations, and that solving the parquet equations yields the best agreement with the NRG benchmark data, but is only feasible up to moderate interaction strengths. Our methodical advances pave the way for treating more complicated models in the future.
Projective symmetry group classification of chiral Z2 spin liquids on the pyrochlore lattice: Application to the spin-1/2 XXZ Heisenberg model
Phys. Rev. B 105, 125122 (2022), B. Schneider, J. C. Halimeh, M. Punk
Simplified models for quantum spin-ice materials, such as the XXZ model on the pyrochlore lattice, may host interesting new spin-liquid ground states. In this work, we provide a complete classification of nearest-neighbor chiral Z2 spin-liquid states on the pyrochlore lattice using a projective symmetry group analysis. Moreover, the newly
classifie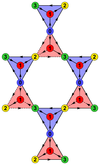 d states are applied to the XXZ model within a self-consistent mean-field scheme. We find a new class of spin-liquid states, the pi/3-states, that inherit their properties from fractionalization of the C3 symmetry of the pyrochlore lattice. Further, we discuss observable signatures that can be measured in neutron scattering experiments. Remarkably, the spin liquids preserve the SU(2) symmetry even in the presence of SU(2) symmetry breaking interactions.
d states are applied to the XXZ model within a self-consistent mean-field scheme. We find a new class of spin-liquid states, the pi/3-states, that inherit their properties from fractionalization of the C3 symmetry of the pyrochlore lattice. Further, we discuss observable signatures that can be measured in neutron scattering experiments. Remarkably, the spin liquids preserve the SU(2) symmetry even in the presence of SU(2) symmetry breaking interactions.
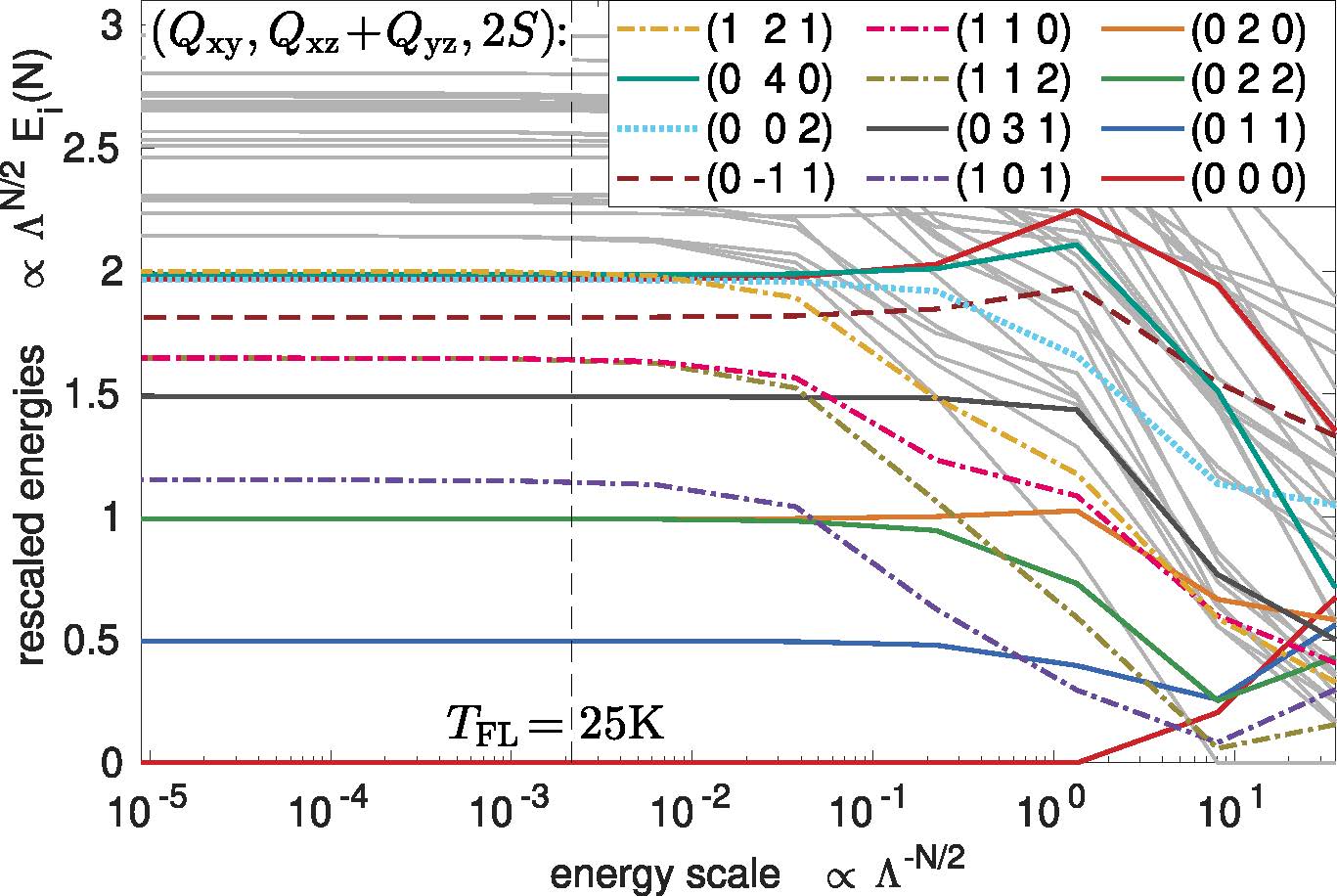
Multipoint Correlation Functions: Spectral Representation and Numerical Evaluation &
Computing Local Multipoint Correlators Using the Numerical Renormalization Group
Phys. Rev. X 11, 041007 (2021), S.-S. B. Lee ,F. B. Kugler, J. von Delft
We show how to compute multipoint correlation functions of quantum many-body systems with unprecedented accuracy. Multipoint functions describe correlations between multiple quantum particles at different space-time points. Such functions pervade many branches of physics and are relevant for interpreting numerous types of experimental measurements, like electrical conductivities and scattering spectra of photons or neutrons. However, multipoint functions are notoriously difficult to compute, especially for strong interactions and low temperatures of interest for understanding quantum systems such as high-temperature superconductors, heavy fermions, or Hund metals.
 In [F. B. Kugler, S.-S. B. Lee, and J. von Delft, Phys. Rev. X 11, 041006 (2021)], we develop a theoretical framework ("spectral representations") expressing general multipoint functions through the system's quantum states, revealing their structure with great clarity. In [S.-S. B. Lee, F. B. Kugler, and J. von Delft, Phys. Rev. X 11, 041007 (2021)], we devise a powerful method for numerically evaluating the spectral representations of local multipoint functions. With this, we compute effective two-particle interactions ("vertex functions") and, as an example, spectra for resonant inelastic x-ray scattering (RIXS), a promising experimental tool in solid-state physics. Our novel approach allows us to accurately treat energies and temperatures ranging over many orders of magnitude, beyond the reach of other numerical methods. This makes it a valuable addition to the toolbox of theoretical techniques for studying quantum matters.
In [F. B. Kugler, S.-S. B. Lee, and J. von Delft, Phys. Rev. X 11, 041006 (2021)], we develop a theoretical framework ("spectral representations") expressing general multipoint functions through the system's quantum states, revealing their structure with great clarity. In [S.-S. B. Lee, F. B. Kugler, and J. von Delft, Phys. Rev. X 11, 041007 (2021)], we devise a powerful method for numerically evaluating the spectral representations of local multipoint functions. With this, we compute effective two-particle interactions ("vertex functions") and, as an example, spectra for resonant inelastic x-ray scattering (RIXS), a promising experimental tool in solid-state physics. Our novel approach allows us to accurately treat energies and temperatures ranging over many orders of magnitude, beyond the reach of other numerical methods. This makes it a valuable addition to the toolbox of theoretical techniques for studying quantum matters.
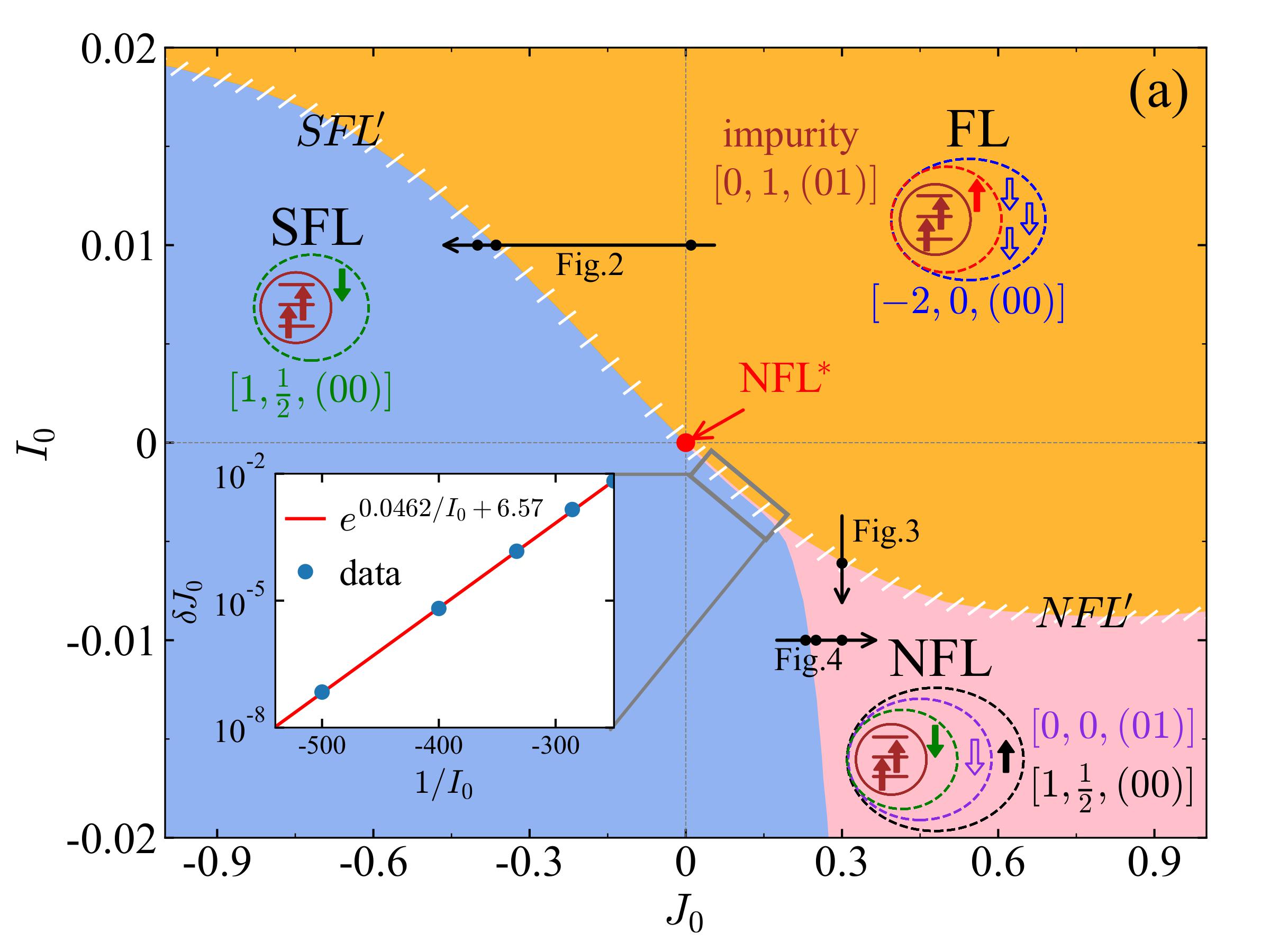
Uncovering Non-Fermi-Liquid Behavior in Hund Metals: Conformal Field Theory Analysis of an SU(2)×SU(3) Spin-Orbital Kondo Model,
Phys. Rev. X 10, 031052 (2020), A. M. Tsvelik 1 and O. M. Yevtushenko
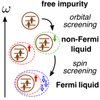 Hund metals have attracted attention in recent years due to their unconventional superconductivity, which supposedly originates from non-Fermi-liquid (NFL) properties of the normal state. When studying Hund metals using dynamical mean-field theory (DMFT), one arrives at a self-consistent "Hund impurity problem" involving a multiorbital quantum impurity with nonzero Hund coupling interacting with a metallic bath. If its spin and orbital degrees of freedom are screened at different energy scales, the intermediate energy window is governed by a novel NFL fixed point, whose nature had not yet been clarified. We resolve this problem by providing an analytical solution of a paradigmatic example of a Hund impurity problem, involving two spin and three orbital degrees of freedom. To this end, we combine a state-of-the-art implementation of the numerical renormalization group, capable of exploiting non-Abelian symmetries, with a generalization of Affleck and Ludwig’s conformal field theory (CFT) approach for multichannel Kondo models.
Hund metals have attracted attention in recent years due to their unconventional superconductivity, which supposedly originates from non-Fermi-liquid (NFL) properties of the normal state. When studying Hund metals using dynamical mean-field theory (DMFT), one arrives at a self-consistent "Hund impurity problem" involving a multiorbital quantum impurity with nonzero Hund coupling interacting with a metallic bath. If its spin and orbital degrees of freedom are screened at different energy scales, the intermediate energy window is governed by a novel NFL fixed point, whose nature had not yet been clarified. We resolve this problem by providing an analytical solution of a paradigmatic example of a Hund impurity problem, involving two spin and three orbital degrees of freedom. To this end, we combine a state-of-the-art implementation of the numerical renormalization group, capable of exploiting non-Abelian symmetries, with a generalization of Affleck and Ludwig’s conformal field theory (CFT) approach for multichannel Kondo models.