Instability of spatial patterns and its ambiguous impact on species diversity
Tobias Reichenbach and Erwin Frey
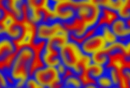
Biodiversity in ecological systems is often maintained by self-arrangement of the interacting individuals into spatial patterns. In our article, we investigate the effects of such self-organizing spatial patterns theoretically, and find that, in most cases, they support species diversity. However, we also identify a situation where a convective (Eckhaus) instability of patterns results in rapid species extinction.
Our work builds on recent microbial experiments. There, three strains of colicinogenic /Escherichia coli/ display a competition similar to the children's game "rock-paper-scissors". Growing on a (essentially two-dimensional) Petri dish, spatial patterns form. In each spatial region, one of the three strains dominates. These patterns help to protect one strain from the others, and therefore enable stable coexistence, in other words, the diversity. In our theoretical work, we investigate a more general situation where three species exhibit cyclic dominance. We demonstrate that, in most cases, the formation of spatial patterns helps the maintenance of biodiversity (see Figure). In contrast, and for the first time, we also show that in a certain regime, the opposite is true: the self-formation of patterns leads to rapid extinction of all but one species. We provide a fundamental understanding of both effects in terms of an analytical description via a complex Ginzburg-Landau equation.