Active research topics

Spin liquids and frustration in Centred Pyrochlore Lattice

group researchers : Tomas Kreißel, Lechen Xu, Lode Pollet

associated members: Naïmo Davier, Ludovic D. C. Jaubert,

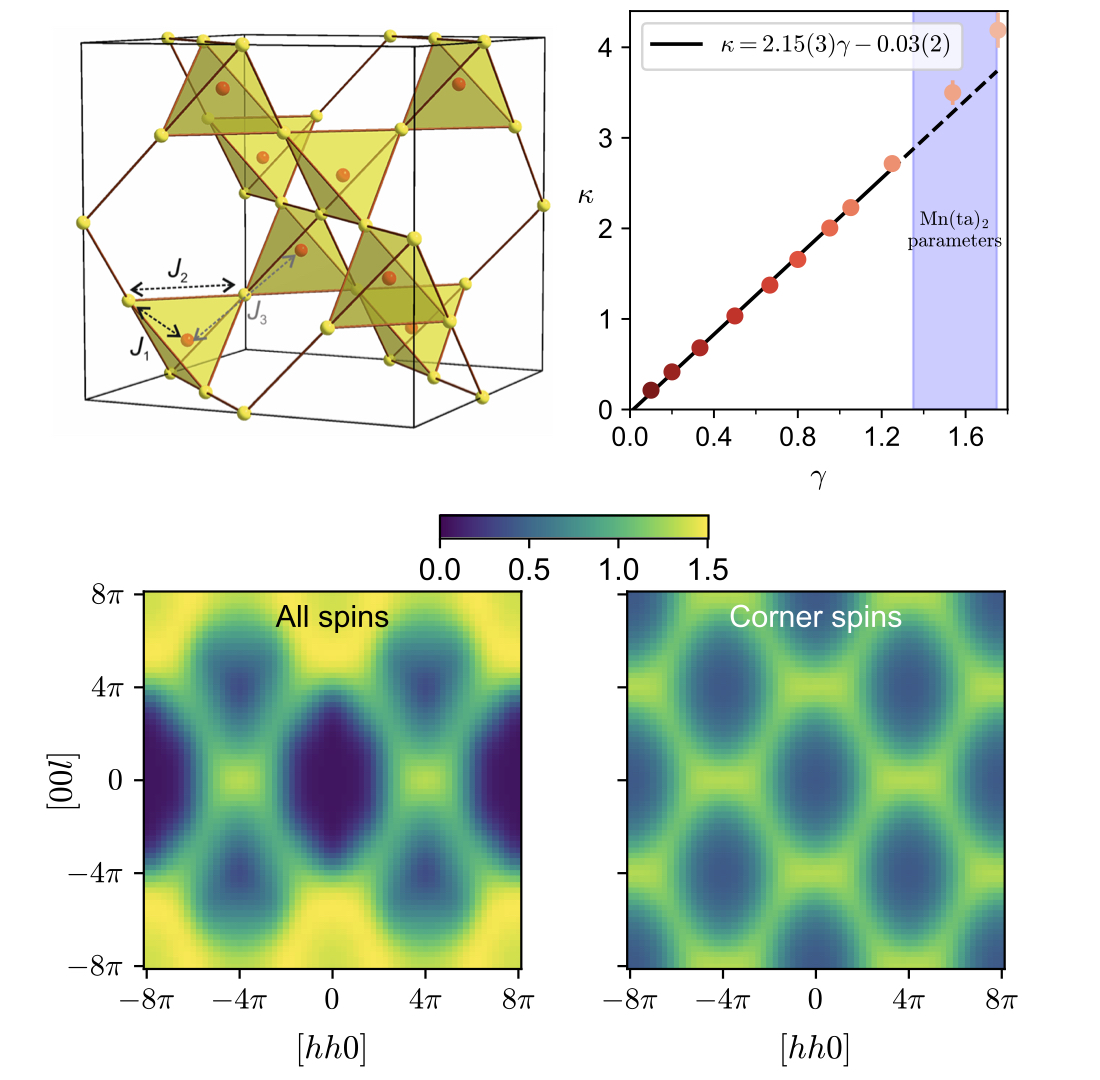The centred pyrochlore lattice is a novel highly geometrically frustrated model characterized by a rich phase diagram at low temperature. This was identified as the molecular design in metal-azolate framework [Mn(II)(ta)2], with the frustrated regime depending on the interplay between nearest neighbour and next-to nearest neighbour interactions (respectively with interaction strength J1 and J2). Through a combination of analytics, numerics and experiments we found that, at a particular interaction regime, the reciprocal space structure factor S(q) is characterized by finite width bowties, also referred to as pinch points, which are found to arise from the correlations between spins residing at the vertices of the tetrahedra. The width of these bowties was found to scale linearly with the ratio γ ≡ J1 /J2 up to γ=1.25. We are currently studying the properties of other, more qunatum MOFs defined on the pyrochlore lattice, as well as the quantum properties of 2D centered lattices such as the centered Kagome lattice.

 References:

• Phys. Rev. B 112, 144437 (2025)

Many-Body physics meets digital qantum computing hardware

group researchers : Alberto Cavallar, Francesco Nappi, Lode Pollet

The group actively participates in finding applications of strongly-correlated many-body physics to digital quantum hardware. We implemented symmetry protected phases (SPT) on trapped ion experiments in collaboration with the University of Innsbruck through the cluster model and MPS representations of spin-1 Haldane order. Our previously developed machine learning algorithm (TK-SVM) was then able to learn their string order parameters without prior supervision and unambiguously discriminate them from topologically trivial phases. We are also interested in computing thresholds for quantum error correction, as well as embedding impurity models self-consistently on quantum hardware (see figure)

References:

• Phys. Rev. Lett. 129, 230502 (2022)
• Phys. Rev. Research 6, 013304 (2024)
• arXiv:2512.22888
• arXiv:2408.05017 (2024)

Quantum spin Lakes in quantum simulators studied with neural quantum states and quantum Monte Carlo states

group researchers : Ali Otaifi, Yaxuan Zhang, Jinxin Federico Villadiego Forero, Lode Pollet

associated: N. Y. Yao (Harvard) and his group

Quantum spin liquids are elusive long-range entangled states. Motivated by experiments in Rydberg quantum simulators, recent excitement has centered on the possibility of dynamically preparing a state with quantum spin liquid correlation even when the ground state phase diagram does not exhibit such a topological phase. Understanding the microscopic nature of such quantum spin ``lake'' states and their relationship to equilibrium spin liquid order remains an essential question. Our group studies the equilibrium (through quantum Monte Carlo) and dynamic (through neural quantum network states) properties of such systems for various setups, with the long-term goal of realizing non-abelian anyons in a quantum simulator setup.

 References:

• Phys Rev Lett 134, 086601 (2024)
• arXiv:2512.09040

associated: S. Linsel, A. Bohrdt, F. Grusdt, L. Homeier (LMU- Boulder)

The toric code is a paradigmatic example of lattice Z2 gauge theory. But how to detect such order in a quantum simulator? What is the precise meaning of the equal-time string correlation functions? What is the meaning of (de)confinement and what is the meaning of topological order? How does percolation relate to this quantities? In this research unit we investigate the fundamental questions of Z2 lattice gauge theory, and have provided an open-source quantum Monte Carlo code of the toric code subject to longitudinal and transverse magnetic fields.

References:

Spin Squeezing

group researchers : Lode Pollet

associated researchers: N. Y. Yao (Harvard) and his group

Spin squeezed entanglement enables metrological precision beyond the classical limit. Understood through the lens of continuous symmetry breaking, dipolar spin systems exhibit the remarkable ability to generate spin squeezing via their intrinsic quench dynamics. To date, this understanding has primarily focused on lattice spin systems; in practice however, dipolar spin systems—ranging from ultracold molecules to nuclear spin ensembles and solid-state color centers—often exhibit significant amounts of positional disorder. We develop a theory for scalable spin squeezing in a two-dimensional randomly diluted lattice of quantum dipoles, which naturally realize a dipolar XXZ model. Via extensive quantum Monte Carlo simulations, we map out the phase diagram for finite-temperature XY order, and by extension scalable spin squeezing, as a function of both disorder and Ising anisotropy. As the disorder increases, we find that scalable spin squeezing survives only near the Heisenberg point. We show that this behavior is due to the presence of rare tightly-coupled dimers, which effectively heat the system post-quench. In the case of strongly-interacting nitrogen-vacancy centers in diamond, we demonstrate that an experimentally feasible strategy to decouple the problematic dimers from the dynamics is sufficient to enable scalable spin squeezing.

figure and text after Avi Kaplan-Lipkin et al, https://arxiv.org/pdf/2512.19781

References:

• Nature Physics 20, 1575-1581 (2024)
• arXiv:2512.19781